Graph data structure is a collection of vertices (nodes) and edges
A vertex represents an entity (object)
An edge is a line or arc that connects a pair of vertices in the graph, represents the relationship between entities
Examples
A computer network is a graph with computers are vertices and network connections between them are edges
The World Wide Web is a graph with web pages are vertices and hyperlinks are edges
Types of Graphs
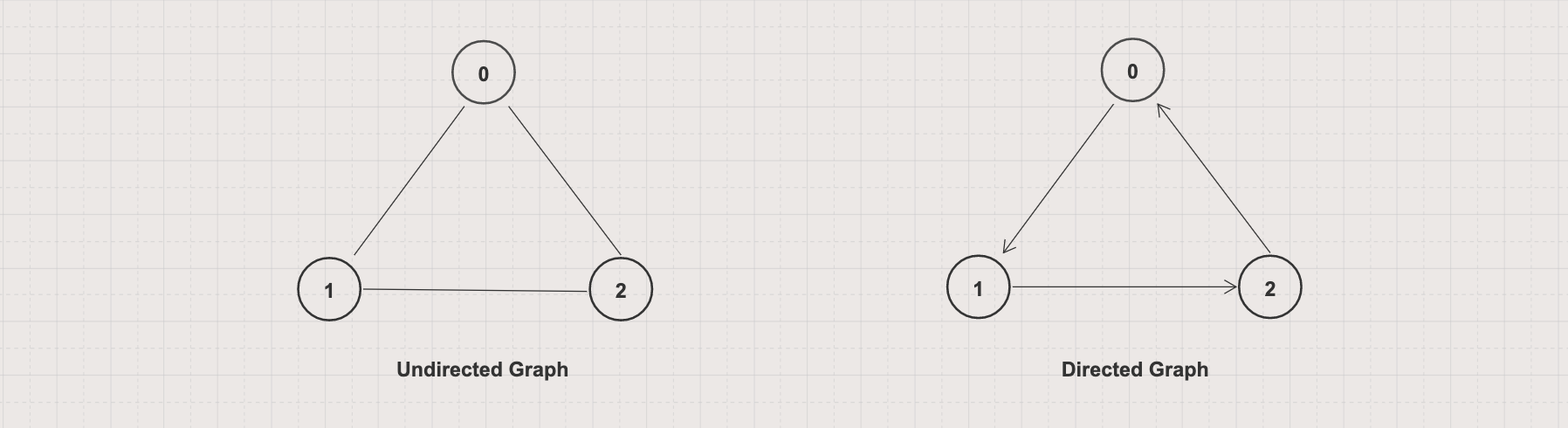
Undirected vs Directed graph
An undirected graph has no directed edges. Every edge in the undirected graph can be travel in both directions (two-way relationships)
A directed graph has no undirected edges. Every edge in the directed graph can be traveled only in a single direction (one-way relationship)
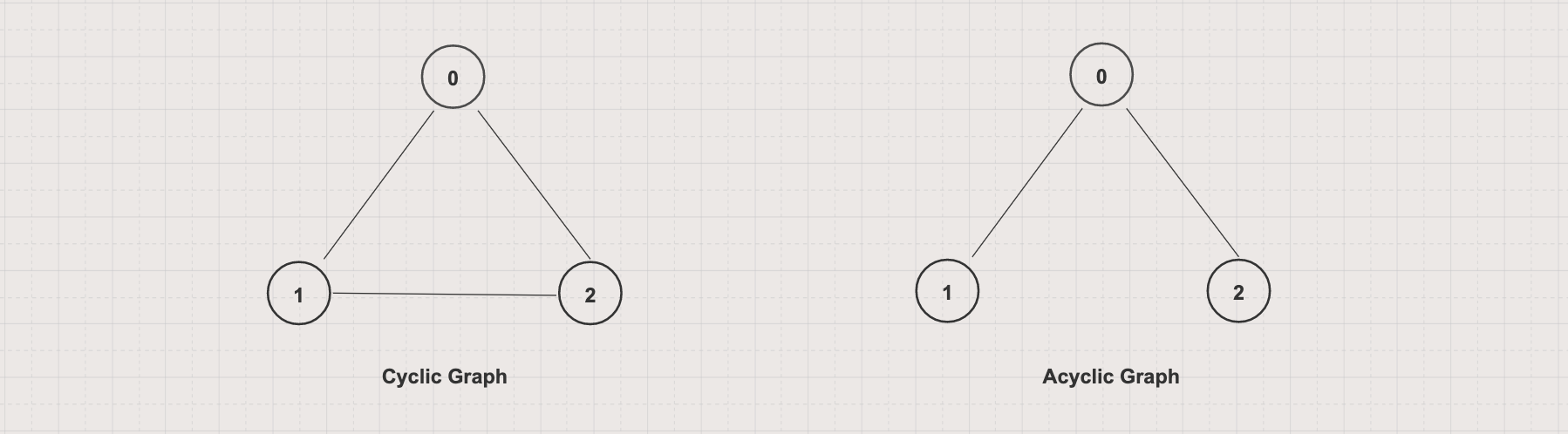
Cyclic vs Acyclic graph
A cyclic graph has at least a cycle (existing a path from at least one node back to itself)
An acyclic graph has no cycles
Connected vs Disconnected graph
A connected graph has no unreachable vertices (existing a path between every pair of vertices)
A disconnected graph has at least an unreachable vertex

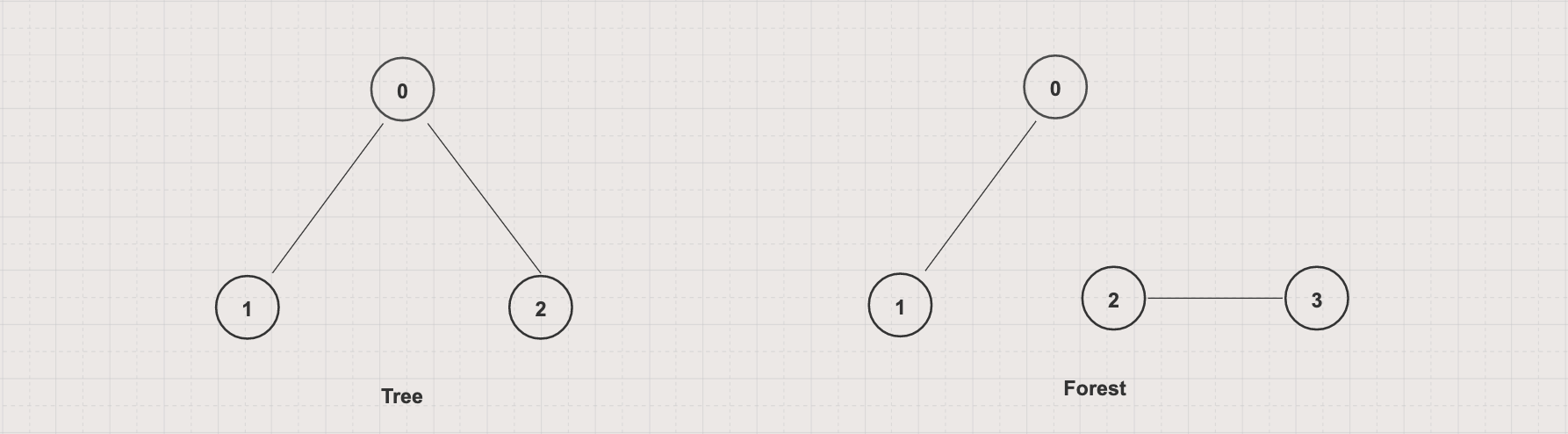
Tree vs Forrest
A tree is a connected acyclic undirected graph
A forest is a graph with each connected component a tree
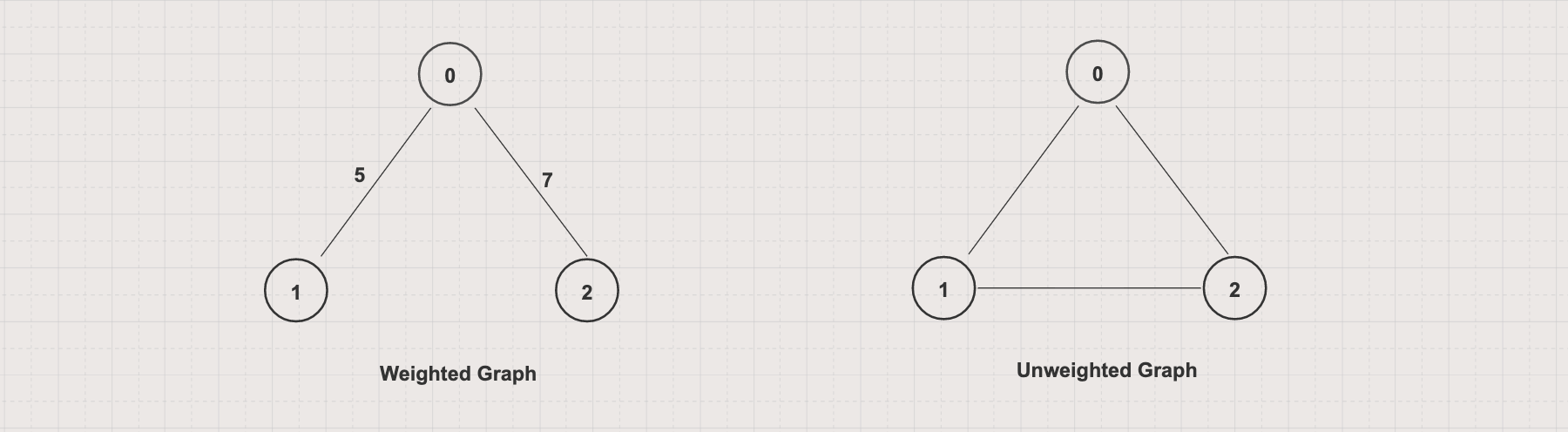
Weighted vs Unweighted graph
A weighted graph has a weight attached to each edge (for example, the distance between two vertices)
An unweighted graph has no weight attached to each edge
Vertex and Graph degree
Verex degree, denoted as deg(v), is a number of edges connected to the vertex. Graph degree, denoted as Δ(G), is the highest vertex degree in a graph
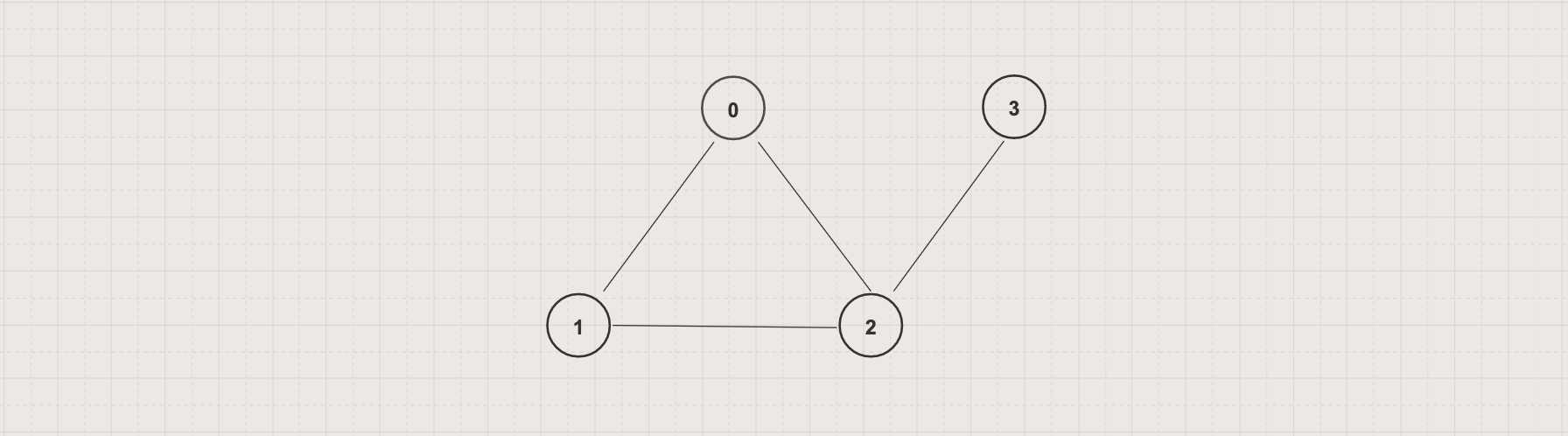
In the above graph
deg(0) = 2, deg(1) = 2, deg(2) = 3, and deg(3) = 1
Δ(G) = 3
Vertex Indegree vs Outdegree
In a directed graph, vertex has an indegree and outdegree
An indegree, denoted as
deg+(v), is a number of edges coming to the vertexAn outdegree, denoted as
deg-(v), is a number of edges leaving the vertex
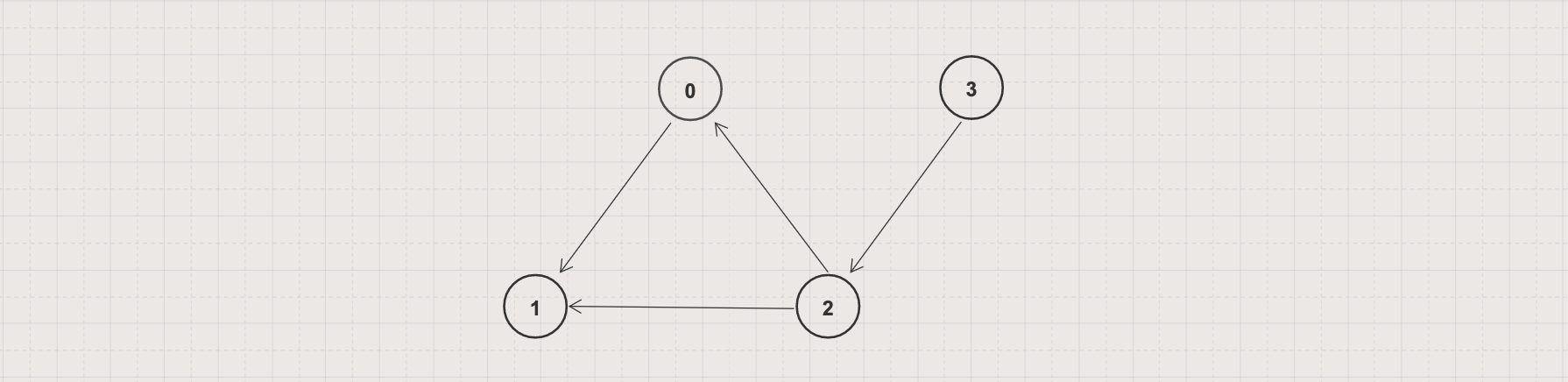
In the above graph
deg+(0) = 1, deg-(0) = 1
deg+(1) = 2, deg-(1) = 0
deg+(2) = 1, deg-(2) = 2
deg+(3) = 0, deg-(3) = 1
Graph Representations
There are several ways to represent a graph including the Edge list, Adjacency list, and Adjacency matrix. Let take this graph as an example

- An edge list is a list or array of all edges where each edge is represented by an array of two vertices
In Java, an edge list can be represented by
int[][] graph = {
{0, 1},
{0, 2},
{1, 2},
{2, 3}
};
An adjacency list is a list or array where index represents a vertex and value represents a list of that vertex's adjacents
In Java, an adjacency list can be represented by
int[][] graph = {
{1, 2},
{0, 2},
{0, 1, 3},
{2}
};
An adjacency matrix is a 2D array of 0s and 1s indicating the connection between two vertices in which the rows represent source vertices and columns represent destination vertices
In Java, an adjacency matrix can be represented by
int[][] graph = {
{0, 1, 1, 0},
{1, 0, 1, 0},
{1, 1, 0, 1},
{0, 0, 1, 0}
};
Basic Graph operations
Add edge: add an edge between two vertices of the graph
Traversal: travel each vertex in the graph by using Depth-Frist and Breath-First Search
Graphs in Java
Java doesn't have a default Graph implementation. However, you can use other supporting data structures to implement it
Undirected vs Directed Graph implementation example
- Undirected graph implementation example with an adjacency list
import java.util.ArrayList;
import java.util.List;
public class GraphUndirectedByAdjacencyList {
private int V;
private List<List<Integer>> adjacencyList;
public GraphUndirectedByAdjacencyList(int V) {
this.V = V;
adjacencyList = new ArrayList<>(V);
for (int i = 0; i < V; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public Integer getV() {
return this.V;
}
public List<List<Integer>> getAdjacencyList() {
return this.adjacencyList;
}
public void addEdge(int source, int dest) {
adjacencyList.get(source).add(dest);
adjacencyList.get(dest).add(source);
}
public void printAdjacencyList() {
for (int i = 0; i < V; i++) {
System.out.printf("Adjacency list of vertex %d is %s %s", i,
adjacencyList.get(i), System.lineSeparator());
}
}
public static void main(String[] args) {
GraphUndirectedByAdjacencyList graph = new GraphUndirectedByAdjacencyList(3);
graph.addEdge(0, 1);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
graph.printAdjacencyList();
}
}
- Directed graph implementation example with an adjacency list
import java.util.ArrayList;
import java.util.List;
public class GraphDirectedByAdjacencyList {
private int V;
private List<List<Integer>> adjacencyList;
public GraphDirectedByAdjacencyList(int V) {
this.V = V;
adjacencyList = new ArrayList<>(V);
for (int i = 0; i < V; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public Integer getV() {
return this.V;
}
public List<List<Integer>> getAdjacencyList() {
return this.adjacencyList;
}
public void addEdge(int source, int dest) {
adjacencyList.get(source).add(dest);
}
public void printAdjacencyList() {
for (int i = 0; i < V; i++) {
System.out.printf("Adjacency list of vertex %d is %s %s", i,
adjacencyList.get(i), System.lineSeparator());
}
}
public static void main(String[] args) {
GraphDirectedByAdjacencyList graph = new GraphDirectedByAdjacencyList(3);
graph.addEdge(0, 1);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
graph.printAdjacencyList();
}
}
- The only difference between the implementations is the
addEdge(source, dest)method.addEdgein an undirected graph adds two-ways direction while in a directed graph adds one-way direction
// addEdge in a directed graph
public void addEdge(int source, int dest) {
adjacencyList[source].add(dest);
}
// addEdge in an undirected graph
public void addEdge(int source, int dest) {
adjacencyList[source].add(dest);
adjacencyList[dest].add(source);
}
Weighted Graph implementation example
- Weighted graph implementation example with an adjacency list
import java.util.ArrayList;
import java.util.List;
public class GraphWeightedByAdjacencyList {
private int V;
private List<List<WeightedVertex>> adjacencyList;
public GraphWeightedByAdjacencyList(int V) {
this.V = V;
adjacencyList = new ArrayList<>(V);
for (int i = 0; i < V; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public Integer getV() {
return this.V;
}
public List<List<WeightedVertex>> getAdjacencyList() {
return this.adjacencyList;
}
public void addEdge(int source, int dest, int weight) {
adjacencyList.get(source).add(new WeightedVertex(dest, weight));
}
public void printAdjacencyList() {
for (int i = 0; i < V; i++) {
System.out.printf("Adjacency list of vertex %d is %s %s", i,
adjacencyList.get(i), System.lineSeparator());
}
}
static class WeightedVertex {
final Integer vertex, weight;
public WeightedVertex(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
public int getWeight() {
return this.weight;
}
public String toString() {
return String.format("%d (weight %d)", vertex, weight);
}
}
public static void main(String[] args) {
GraphWeightedByAdjacencyList g = new GraphWeightedByAdjacencyList(4);
g.addEdge(0, 1, 19);
g.addEdge(2, 0, 15);
g.addEdge(2, 1, 17);
g.addEdge(3, 2, 12);
g.printAdjacencyList();
}
}
Graph traversal and searching with Depth-First and Breadth-First Search
Depth-First Search (DFS) and Breadth-First Search (BFS) are algorithms for traversing or searching a graph
DFS starts at an arbitrary node and explores as far as possible along each branch before backtracking
BFS starts at an arbitrary node and explores all of the neighbor nodes at the current level before moving on to the next level
Thus DFS is better when the target is far from the source while BFS is better when the target is close to the source
DFS uses a Stack while BFS uses a Queue data structure to backtrack vertices on the traversal path
DFS consumes less memory than BFS as BFS has to store all the children at each level
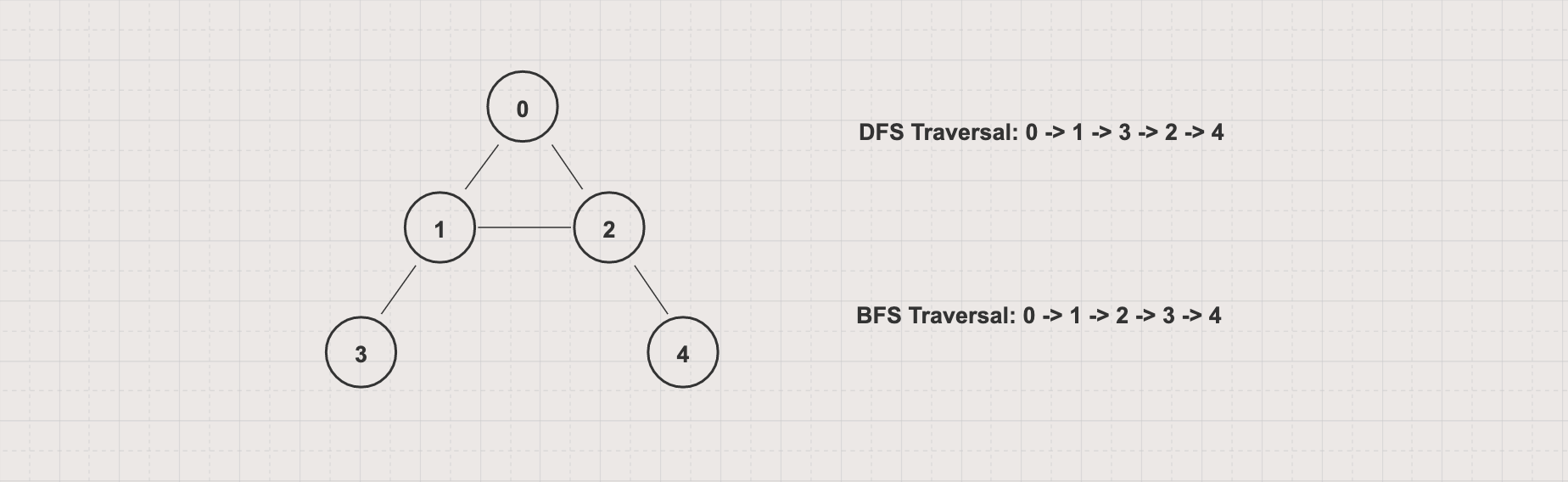
Learn more about Depth-First Search and Breadth-First Search
Detect Cycle in a Directed Graph
You can use DFS to detect a cycle in a directed graph. When visiting a vertex v and its adjacency vertices, if there is a back edge (w, v) which directs to v then that graph has a cycle
Topological Sort with Directed Acyclic Graph
Topological sort is an algorithm which takes a directed acyclic graph and returns a list of vertices in the linear ordering where each vertex has to precede all vertices it directs to
DFS and the above vertex degree theory can be used to implement the topological sort
Find shortest paths between vertices
The shortest path is a path between two vertices in a graph such that the total sum of the weights of the constituent edges is minimum
You can implement an algorithm to find the shortest path by using Breadth-First Search (BFS), Dijkstra, Bellman-Ford, and Floyd-Warshall algorithms
