In this article, we will learn to implement a Breadth-First Search (BFS) algorithm example on a graph in Java

Breadth-First Search (BFS) is an algorithm for traversing or searching on a graph or tree layer-wise. It starts at an arbitrary node and explores all of the neighbor nodes before moving to the next depth level

Problem

  • Give an undirected/directed graph G(V, E) where V is the list of vertex and E is the list of edges

  • Write a Breadth-First search algorithm to print out each vertex value exactly once

Example

  • Input: Given an undirected graph G(V,E) with V = [0, 1, 2, 3, 4] and E = [[0, 1], [0, 2], [1, 2], [1, 3], [2, 4]]

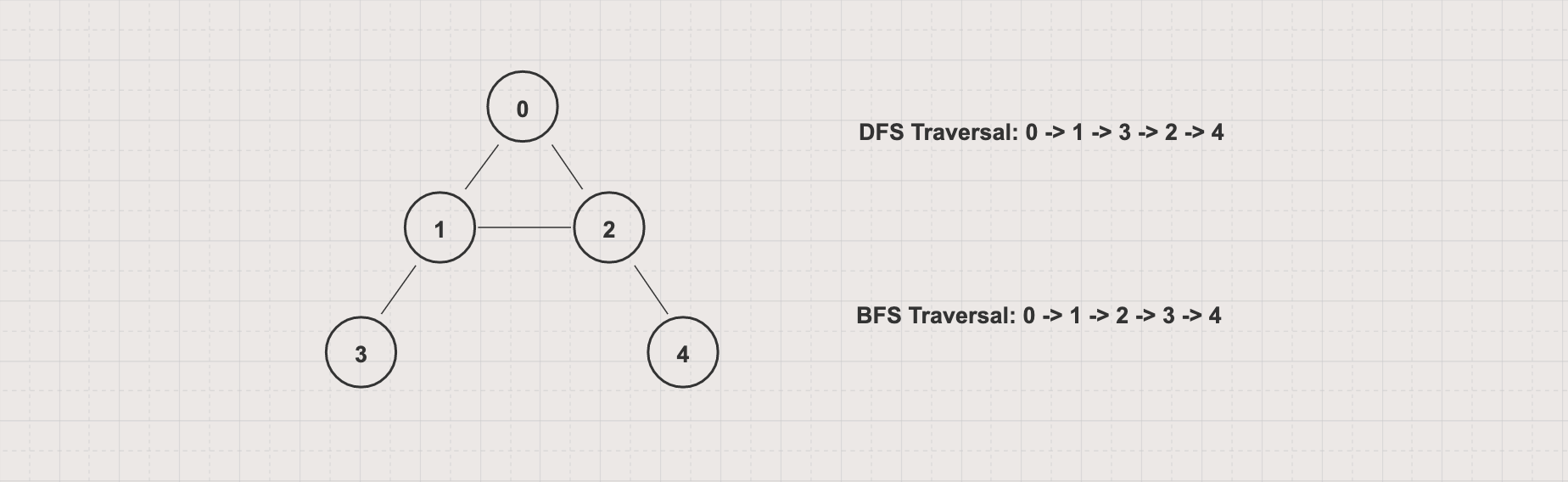
  • Ouput: For the above graph with 0 as the starting vertex, assuming that the left edges are chosen before the right edges, the BFS traversal order will be 0 -> 1 -> 2 -> 3 -> 4, so the expected output will be 0 1 2 3 4

Approach 1: Boolean Array and FIFO Queue

  • Create a boolean array to track visited nodes to avoid processing a node more than once. Each node can have 2 states: visited or unvisited

  • Create a FIFO queue to track which nodes to visit next on the traversal path. Add the starting node into the queue

  • Do the following while the queue is still containing items

    • Retrieves and removes a node from the queue

    • If the node has yet to be visited, change its state to visited in the boolean array, print out its value, and add all of its neighbour nodes into the queue

import java.util.ArrayDeque;  
import java.util.Deque;

public class BFSByIterative {  
    public static void bfsByIterative(GraphUndirectedByAdjacencyList g, int v) {
        boolean[] visited = new boolean[g.getV()];
        Deque<Integer> queue = new ArrayDeque<>();
        queue.offer(v);

        while (!queue.isEmpty()) {
            v = queue.poll();

            if (!visited[v]) {
                visited[v] = true;
                System.out.printf("%d ", v);

                for (Integer w : g.getAdjacencyList().get(v)) {
                    queue.offer(w);
                }
            }
        }
    }

    public static void main(String[] args) {
        GraphUndirectedByAdjacencyList g = new GraphUndirectedByAdjacencyList(5);
        g.addEdge(0, 1);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(1, 3);
        g.addEdge(2, 4);

        bfsByIterative(g, 0);
    }
}

GraphUndirectedByAdjacencyList is defined in Graph Data Structure

  • Output
0 1 2 3 4
  • Time complexity is O(V+E) and space complexity is O(V), where V is the number of nodes and E is the number of edges in the given graph

Approach 2: Color Array and FIFO Queue

  • Create a color array to track vertex states. Each vertex can have 3 states marked by color

    • White represents unvisited

    • Gray represents a visit in progress

    • Black represents visited

  • Create a FIFO queue to track which nodes to visit next on the traversal path

  • Do the following while the queue is still containing items

    • Retrieves and removes a node from the queue

    • If the node has white color, change it to gray, print out its value, add all of its neighbour nodes into the queue, and change the node color to black

import java.util.ArrayDeque;  
import java.util.Deque;

public class BFSByIterativeWithColor {  
    static final int WHITE = 0, GRAY = 1, BLACK = 2;

    public static void bfsByIterativeWithColor(GraphUndirectedByAdjacencyList g, int v) {
        int[] color = new int[g.getV()];
        Deque<Integer> queue = new ArrayDeque<>();
        queue.offer(v);

        while (!queue.isEmpty()) {
            v = queue.poll();

            if (color[v] == WHITE) {
                color[v] = GRAY;
                System.out.printf("%d ", v);

                for (Integer w : g.getAdjacencyList().get(v)) {
                    queue.offer(w);
                }

                color[v] = BLACK;
            }
        }
    }

    public static void main(String[] args) {
        GraphUndirectedByAdjacencyList g = new GraphUndirectedByAdjacencyList(5);
        g.addEdge(0, 1);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(1, 3);
        g.addEdge(2, 4);

        bfsByIterativeWithColor(g, 0);
    }
}

GraphUndirectedByAdjacencyList is defined in Graph Data Structure

  • Output
0 1 2 3 4
  • Time complexity is O(V+E) and space complexity is O(V), where V is the number of nodes and E is the number of edges in the given graph

Applications

Algorithm