The shortest path algorithm finds paths between two vertices in a graph such that total sum of the constituent edge weights is minimum
In the following graph, between vertex 3 and 1, there are two paths including [3, 2, 1] costs 9 (4 + 5) and [3, 2, 0, 1] costs 7 (4 + 1 + 2). The shortest path is [3, 2, 0, 1]
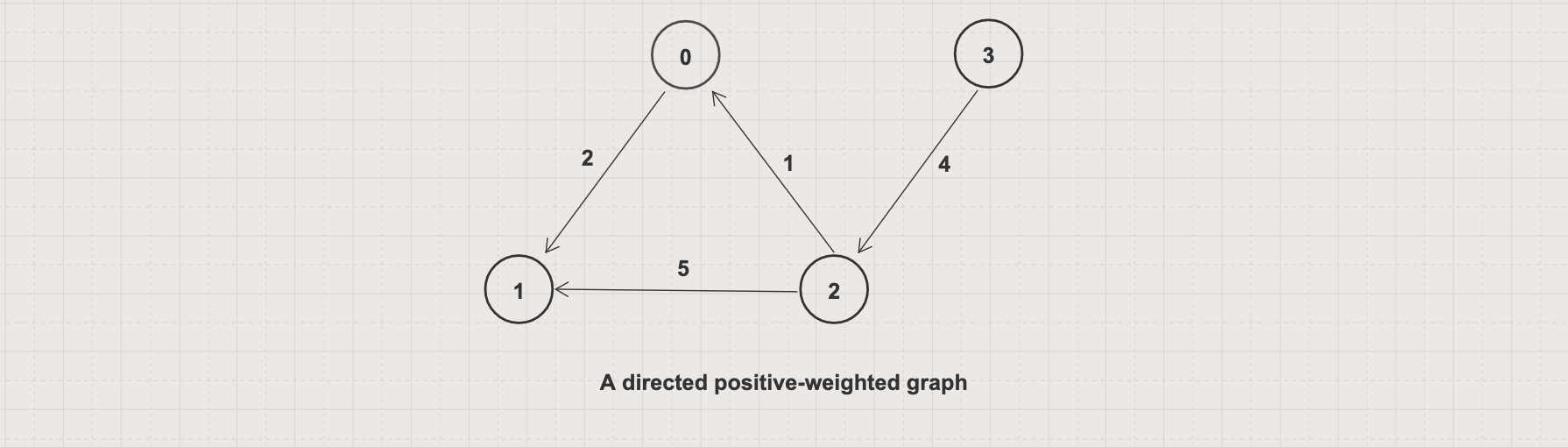
In this article, you will learn to implement the Shortest Path Algorithms with Breadth-First Search (BFS), Dijkstra, Bellman-Ford, and Floyd-Warshall algorithms
BFS algorithm is used to find the shortest paths from a single source vertex in an unweighted graph
Dijkstra algorithm is used to find the shortest paths from a single source vertex in a nonnegative-weighted graph
Bellman-Ford and Floyd-Warshall algorithms are used to find the shortest paths in a negative-weighted graph which has both non-negative and negative weights. While Bellman-Ford is used to find from a single source vertex, Floyd-Warshall is used to find from all pairs of vertices
Edge Relaxation
Dijkstra and Bellman-Ford algorithms work based on a technique known as edge relaxation which is an analogy to the process of repeatedly improving the shortest path approximations from a source vertex s to every vertex v in a graph
Problem 1: Single-source Shortest Paths in an Unweighted Graph
Given an unweighted graph G = (V, E) and a single source vertex s in V
Write an algorithm to find the shortest path from s to every vertex in V
Example 1
- Input: Given a directed unweighted graph G = (V, E) with V = 4 and E = [[0, 1], [2, 0], [2, 1], [3, 2]]
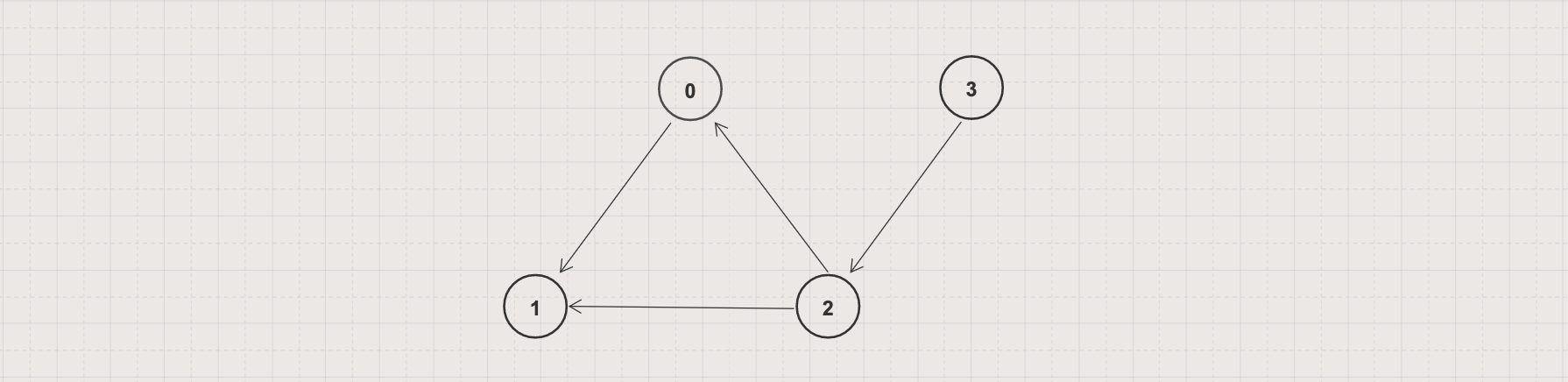
- Output 1: With the finding started at source vertex s = 3
Vertex Distance from source Route from source
0 2 [3, 2, 0]
1 2 [3, 2, 1]
2 1 [3, 2]
3 0 [3]
- Output 2: With the finding started at source vertex s = 2
Vertex Distance from source Route from source
0 1 [2, 0]
1 1 [2, 1]
2 0 [2]
3 N/A N/A
Approach 1: BFS Algorithm
In the above example, to calculate the distance from the source vertex 3 to 1, you can compute and combine the distance from 3 to 2 and 2 to 1
Lets use an array d[V] to store the approximate distance from s to every vertex v in V. Init d[v] = Infinity value for every vertex v, except d[s] = 0, then
d[3] = 0
d[2] = d[3] + 1 = 1
d[1] = d[2] + 1 = 2
d[0] = d[2] + 1 = 2
In general, d[v] = d[u] + 1 for every edge (u, v) in the graph
import java.util.*;
public class ShortestPathByBFS {
static final int INFINITE = Integer.MAX_VALUE;
static final int UNDEFINED = -1;
public static Object[] shortestPathByBFS(GraphDirectedByAdjacencyList g, int source) {
int[] distances = new int[g.getV()];
int[] predecessors = new int[g.getV()];
for (int v = 0; v < g.getV(); v++) {
distances[v] = INFINITE;
predecessors[v] = UNDEFINED;
}
distances[source] = 0;
boolean[] visited = new boolean[g.getV()];
visited[source] = true;
Queue<Integer> queue = new ArrayDeque<>();
queue.offer(source);
while (!queue.isEmpty()) {
int u = queue.poll();
for (int v : g.getAdjacencyList().get(u)) {
if (!visited[v]) {
visited[v] = true;
distances[v] = distances[u] + 1;
predecessors[v] = u;
queue.offer(v);
}
}
}
return new Object[]{distances, predecessors};
}
static void printResult(Object[] paths) {
int[] distancesFromSource = (int[]) paths[0];
int[] predecessorsOfSource = (int[]) paths[1];
System.out.println("Vertex\tDistance from source\tRoute from source");
for (int v = 0; v < distancesFromSource.length; v++) {
if (distancesFromSource[v] == INFINITE) {
System.out.printf("%-8s%-24s%s%s", v, "N/A", "N/A", System.lineSeparator());
continue;
}
Deque<Integer> route = new ArrayDeque<>();
route.push(v);
int u = predecessorsOfSource[v];
while (u >= 0) {
route.push(u);
u = predecessorsOfSource[u];
}
System.out.printf("%-8d%-24d%s%s", v, distancesFromSource[v], route.toString(), System.lineSeparator());
}
}
public static void main(String[] args) {
GraphDirectedByAdjacencyList g = new GraphDirectedByAdjacencyList(4);
g.addEdge(0, 1);
g.addEdge(2, 0);
g.addEdge(2, 1);
g.addEdge(3, 2);
printResult(shortestPathByBFS(g, 3));
printResult(shortestPathByBFS(g, 2));
}
}
GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial
Time complexity: O(V+E)
Space complexity: O(V)
Problem 2: Single-source Shortest Paths in a NonNegative-Weighted Graph
Given a nonnegative-weighted graph G = (V, E) and a single source vertex s in V
Write an algorithm to find the shortest path from s to every vertex in V
Example 2
- Input: Given a directed nonnegative-weighted graph G = (V, E) with V = 4 and E = [[0, 1, 2], [2, 0, 1], [2, 1, 5], [3, 2, 4]]

- Output: With the finding started at source vertex s = 3
Vertex Distance from source Route from source
0 5 [3, 2, 0]
1 7 [3, 2, 0, 1]
2 4 [3, 2]
3 0 [3]
- Output: With the finding started at source vertex s = 2
Vertex Distance from source Route from source
0 1 [2, 0]
1 3 [2, 0, 1]
2 0 [2]
3 N/A N/A
Why BFS doesn't work on a weighted graph? Says you find the shortest path from 3 to 1
BFS: [3, 2, 1] costs 9
Shortest path (minimum cost path): [3, 2, 0, 1] costs 7
Approach 2.1: Dijkstra Algorithm
- Let's use an array d[V] to store the approximate distance from s to every vertex v in V. Init d[v] = Infinity value for every vertex v, except d[s] = 0, then with the above example
d[3] = 0
for edge (3, 2), d[2] = min(d[2], d[3] + 4)
for edge (2, 0), d[0] = min(d[0], d[2] + 1)
for edge (2, 1), d[1] = min(d[1], d[2] + 5)
for edge (0, 1), d[1] = min(d[1], d[0] + 2)
In general, d[v] = min(d[v], d[u] + weight(u,v)) for every edge (u, v) in the graph
import java.util.*;
import static com.hellokoding.datastructure.graph.GraphWeightedByAdjacencyList.WeightedVertex;
public class ShortestPathByDijkstra {
static final int INFINITE = Integer.MAX_VALUE;
static final int UNDEFINED = -1;
static int minVertex(Queue<Integer> queue, int[] distance) {
int minDistance = INFINITE;
int minVertex = UNDEFINED;
for (Integer v : queue) {
if (minDistance > distance[v]) {
minDistance = distance[v];
minVertex = v;
}
}
return minVertex;
}
static Object[] shortestPathByDijkstra(GraphWeightedByAdjacencyList g, int source) {
int[] distances = new int[g.getV()];
int[] predecessors = new int[g.getV()];
Queue<Integer> queue = new ArrayDeque<>();
for (int v = 0; v < g.getV(); v++) {
distances[v] = INFINITE;
predecessors[v] = UNDEFINED;
queue.offer(v);
}
distances[source] = 0;
while (!queue.isEmpty()) {
int u = minVertex(queue, distances);
if (u == UNDEFINED) break;
queue.remove(u);
for (WeightedVertex v : g.getAdjacencyList().get(u)) {
if (distances[u] == INFINITE) continue;
int alt = distances[u] + v.weight;
if (alt < distances[v.vertex]) {
distances[v.vertex] = alt;
predecessors[v.vertex] = u;
}
}
}
return new Object[]{distances, predecessors};
}
static void printResult(Object[] paths) {
int[] distances = (int[]) paths[0];
int[] predecessors = (int[]) paths[1];
System.out.println("Vertex\tDistance from source\tRoute from source");
for (int v = 0; v < distances.length; v++) {
if (distances[v] == INFINITE) {
System.out.printf("%-8s%-24s%s%s", v, "N/A", "N/A", System.lineSeparator());
continue;
}
Deque<Integer> route = new ArrayDeque<>();
route.push(v);
int u = predecessors[v];
while (u >= 0) {
route.push(u);
u = predecessors[u];
}
System.out.printf("%-8d%-24d%s%s", v, distances[v], route.toString(), System.lineSeparator());
}
}
public static void main(String[] args) {
GraphWeightedByAdjacencyList g = new GraphWeightedByAdjacencyList(4);
g.addEdge(0, 1, 2);
g.addEdge(2, 0, 1);
g.addEdge(2, 1, 5);
g.addEdge(3, 2, 4);
printResult(shortestPathByDijkstra(g, 3));
printResult(shortestPathByDijkstra(g, 2));
}
}
GraphWeightedByAdjacencyList is defined in Graph Data Structure Tutorial
Time complexity: O(V2)
Space complexity: O(V)
Approach 2.2: Dijkstra Algorithm with Min Heap
- A min-heap (priority queue) is used to greedily pick the unvisited and closest vertex u and perform relaxation for every edge (u, v) comes out from u
import java.util.*;
import static com.hellokoding.datastructure.graph.GraphWeightedByAdjacencyList.WeightedVertex;
public class ShortestPathByDijkstraWithMinHeap {
static final int INFINITE = Integer.MAX_VALUE;
static final int UNDEFINED = -1;
static Object[] shortestPathByDijkstra(GraphWeightedByAdjacencyList g, int source) {
int[] distances = new int[g.getV()];
int[] predecessors = new int[g.getV()];
PriorityQueue<WeightedVertex> minHeap = new PriorityQueue<>(g.getV(), Comparator.comparingInt(WeightedVertex::getWeight));
for (int v = 0; v < g.getV(); v++) {
distances[v] = INFINITE;
predecessors[v] = UNDEFINED;
minHeap.add(new WeightedVertex(v, distances[v]));
}
distances[source] = 0;
while (!minHeap.isEmpty()) {
WeightedVertex u = minHeap.poll();
for (WeightedVertex v : g.getAdjacencyList().get(u.vertex)) {
if (distances[u.vertex] == INFINITE) continue;
int alt = distances[u.vertex] + v.weight;
if (alt < distances[v.vertex]) {
distances[v.vertex] = alt;
predecessors[v.vertex] = u.vertex;
}
}
}
return new Object[]{distances, predecessors};
}
static void printResult(Object[] paths) {
int[] distances = (int[]) paths[0];
int[] predecessors = (int[]) paths[1];
System.out.println("Vertex\tDistance from source\tRoute from source");
for (int v = 0; v < distances.length; v++) {
if (distances[v] == INFINITE) {
System.out.printf("%-8s%-24s%s%s", v, "N/A", "N/A", System.lineSeparator());
continue;
}
Deque<Integer> route = new ArrayDeque<>();
route.push(v);
int u = predecessors[v];
while (u >= 0) {
route.push(u);
u = predecessors[u];
}
System.out.printf("%-8d%-24d%s%s", v, distances[v], route.toString(), System.lineSeparator());
}
}
public static void main(String[] args) {
GraphWeightedByAdjacencyList g = new GraphWeightedByAdjacencyList(4);
g.addEdge(0, 1, 2);
g.addEdge(2, 0, 1);
g.addEdge(2, 1, 5);
g.addEdge(3, 2, 4);
printResult(shortestPathByDijkstra(g, 3));
printResult(shortestPathByDijkstra(g, 2));
}
}
GraphWeightedByAdjacencyList is defined in Graph Data Structure Tutorial
Time complexity: O((E + V) log V)
Space complexity: O(V)
Problem 3: Single-source Shortest Paths in a Negative-Weighted Graph
Given a negative-weighted graph G = (V, E) and a single source vertex s in V
Write an algorithm to find the shortest path from s to every vertex in V
Returns an error message if the input graph has a negative weight cycle
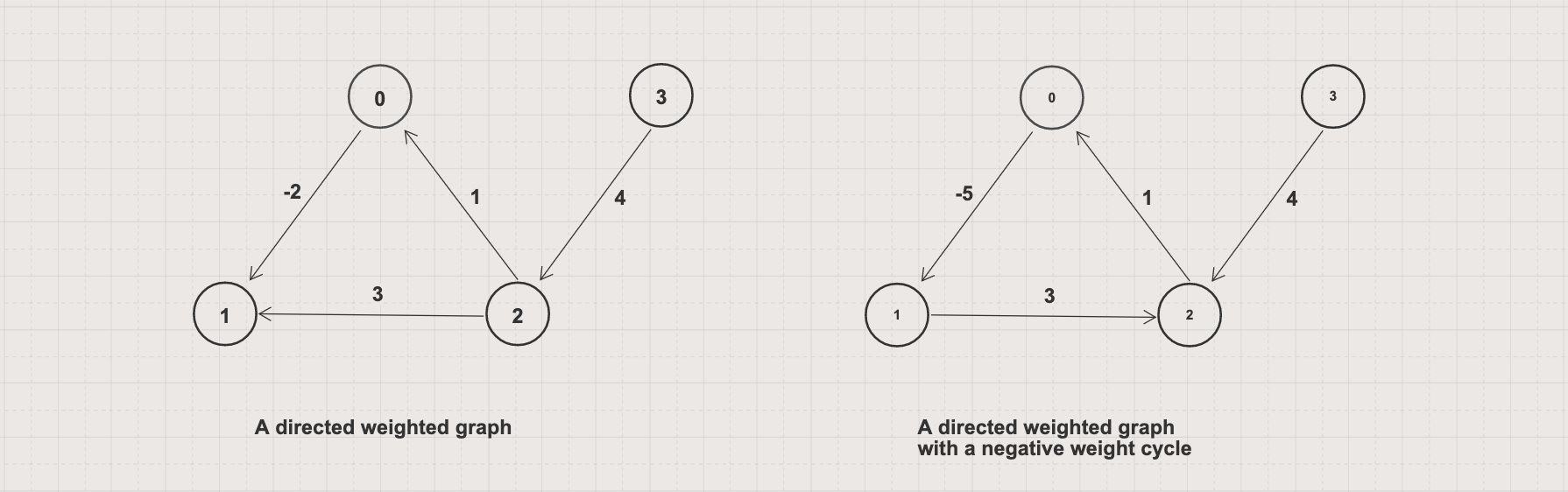
Example 3.1
Input: Given a directed graph G = (V, E) with V = 4 and E = [[0, 1, -2], [2, 0, 1], [2, 1, 3], [3, 2, 4]]
Output: With the finding started at source vertex s = 3
Vertex Distance from source Route from source
0 5 [3, 2, 0]
1 3 [3, 2, 0, 1]
2 4 [3, 2]
3 0 [3]
Example 3.2
Input: Given a directed graph G = (V, E) with V = 4 and E = [[0, 1, -5], [2, 0, 1], [1, 2, 3], [3, 2, 4]]
Output: With the finding started at any source vertex
The input graph contains a negative-weight cycle
Approach 3: Bellman-Ford Algorithm
In the first example, from source vertex 3 to 1, there are 2 paths [3, 2, 1] costs 7 (4 + 3) and [3, 2, 0, 1] costs 3 (4 + 1 - 2), the shortest path is [3, 2, 0, 1]
Let's use an array d[V] to store the approximate distance from s to every vertex v in V. Init d[v] = Infinity value for every vertex v, except d[s] = 0, then with the above example
d[3] = 0
for edge (3, 2), d[2] = min(d[2], d[3] + 4)
for edge (2, 0), d[0] = min(d[0], d[2] + 1)
for edge (2, 1), d[1] = min(d[1], d[2] + 3)
for edge (0, 1), d[1] = min(d[1], d[0] - 2)
In general, d[v] = min(d[v], d[u] + weight(u,v)) for every edge (u, v) in the graph
Bellman-Ford algorithm doesn't work with a negative-weighted cycle. In the second example, 3 edges (2, 0), (0, 1), and (1, 0) forms a negative-weighted cycle (sum of weights is -1)
Dijkstra algorithm uses a priority queue to greedily pick the unvisited and closest vertex u and perform relaxation for every edge (u, v) comes out from u. Bellman-Ford algorithm doesn't use a queue, but do the relaxation for all edges V-1 times
Bellman-Ford algorithm is slower but more versatile than Dijkstra algorithm as it can work with negative weight edges
import java.util.*;
public class ShortestPathByBellmanFord {
static final int INFINITE = Integer.MAX_VALUE;
static final int UNDEFINED = -1;
static Object[] shortestPathByBellmanFord(GraphWeightedByAdjacencyList g, int source) {
int[] distances = new int[g.getV()];
int[] predecessors = new int[g.getV()];
for (int v = 0; v < g.getV(); v++) {
distances[v] = INFINITE;
predecessors[v] = UNDEFINED;
}
distances[source] = 0;
for (int i = 1; i < g.getV(); i++) {
for (int u = 0; u < g.getV(); u++) {
for (GraphWeightedByAdjacencyList.WeightedVertex v : g.getAdjacencyList().get(u)) {
if (distances[u] == INFINITE) continue;
int alt = distances[u] + v.weight;
if (alt < distances[v.vertex]) {
distances[v.vertex] = alt;
predecessors[v.vertex] = u;
}
}
}
}
for (int u = 0; u < g.getV(); u++) {
for (GraphWeightedByAdjacencyList.WeightedVertex v : g.getAdjacencyList().get(u)) {
if (distances[u] == INFINITE) continue;
int alt = distances[u] + v.weight;
if (alt < distances[v.vertex]) {
System.out.println("The input graph contains a negative-weight cycle");
return new Object[]{};
}
}
}
return new Object[]{distances, predecessors};
}
static void printResult(Object[] paths) {
if (paths.length == 0) return;
int[] distances = (int[]) paths[0];
int[] predecessors = (int[]) paths[1];
System.out.println("Vertex\tDistance from source\tRoute from source");
for (int v = 0; v < distances.length; v++) {
if (distances[v] == INFINITE) {
System.out.printf("%-8s%-24s%s%s", v, "N/A", "N/A", System.lineSeparator());
continue;
}
Deque<Integer> route = new ArrayDeque<>();
route.push(v);
int u = predecessors[v];
while (u >= 0) {
route.push(u);
u = predecessors[u];
}
System.out.printf("%-8d%-24d%s%s", v, distances[v], route.toString(), System.lineSeparator());
}
}
public static void main(String[] args) {
GraphWeightedByAdjacencyList g1 = new GraphWeightedByAdjacencyList(4);
g1.addEdge(0, 1, -2);
g1.addEdge(2, 0, 1);
g1.addEdge(2, 1, 3);
g1.addEdge(3, 2, 4);
printResult(shortestPathByBellmanFord(g1, 3));
GraphWeightedByAdjacencyList g2 = new GraphWeightedByAdjacencyList(4);
g2.addEdge(0, 1, -5);
g2.addEdge(2, 0, 1);
g2.addEdge(1, 2, 3);
g2.addEdge(3, 2, 4);
printResult(shortestPathByBellmanFord(g2, 3));
}
}
GraphWeightedByAdjacencyList is defined in Graph Data Structure Tutorial
Time complexity: O(VE)
Space complexity: O(V)
Problem 4: All-pairs Shortest Paths in a Negative-Weighted Graph
Given a negative-weighted graph G = (V, E) and a single source vertex s in V
Write an algorithm to find the shortest path from all-pairs of vertices in V
Returns an error message if the input graph has a negative weight cycle

Example 4.1
- Input: Given a directed graph G which represented as the following matrix, I denotes the infinity value
0 -2 I I
I 0 I I
1 3 0 I
I I 4 0
- Output: With the finding started from all-pairs of vertices
0 -2 I I
I 0 I I
1 -1 0 I
5 3 4 0
Example 4.2
- Input: Given a directed graph G which represented as the following matrix, I denotes the infinity value
0 -5 I I
I 0 3 I
1 I 0 I
I I 4 0
- Output: With the finding started from all-pairs of vertices
The input graph contains a negative-weight cycle
Approach 4: Floyd-Warshall Algorithm
The algorithm incrementally improving an estimate on the shortest path between all pairs of vertices (i, j) by comparing all possible paths between the pair
For each pair of vertices (i, j), the shortest path between them is a min value of the path from i to j and the paths between i to k and k to j with k are intermediate vertices
Floyd-Warshall algorithm doesn't work with a negative-weighted cycle. In the second example, 3 edges (2, 0), (0, 1), and (1, 0) forms a negative-weighted cycle (sum of weights is -1)
import java.util.Arrays;
public class ShortestPathByFloydWarshall {
static final int I = Integer.MAX_VALUE;
public static int[][] shortestPathByBFSFloydWarshall(int[][] g) {
int V = g.length;
int[][] distances = Arrays.copyOf(g, V);
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (distances[i][k] == I || distances[k][j] == I) continue;
distances[i][j] = Math.min(distances[i][j], distances[i][k] + distances[k][j]);
}
if (distances[i][i] < 0) {
System.out.println("The input graph contains a negative-weight cycle");
return new int[][]{};
}
}
}
return distances;
}
static void printResult(int[][] distances) {
int V = distances.length;
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
System.out.printf("%-4s", distances[i][j] == I ? "I" : distances[i][j]);
}
System.out.println();
}
System.out.println();
}
public static void main(String[] args) {
int[][] g1 = new int[][] {
{0, -2, I, I},
{I, 0, I, I},
{1, 3, 0, I},
{I, I, 4, 0}
};
printResult(shortestPathByBFSFloydWarshall(g1));
int[][] g2 = new int[][] {
{0, -5, I, I},
{I, 0, 3, I},
{1, I, 0, I},
{I, I, 4, 0}
};
printResult(shortestPathByBFSFloydWarshall(g2));
}
}
Time complexity: O(V3)
Space complexity: O(V)
