In this article, you will learn to implement a Topological sort algorithm by using Depth-First Search and In-degree algorithms
Topological sort is an algorithm which takes a directed acyclic graph and returns a list of vertices in the linear ordering where each vertex has to precede all vertices it directs to
There are no topological orderings exist in a directed cyclic graph and more than one of them can exist in one directed acyclic graph
Problem
Given a directed graph G = (V, E)
Write an algorithm to return a sorted vertex list in topological ordering
Return an empty list if no topological orderings exist
Example 1
- Input: Given a directed graph G = (V, E) with V = 4 and E = [[0, 1], [2, 0], [2, 1], [3, 2]]
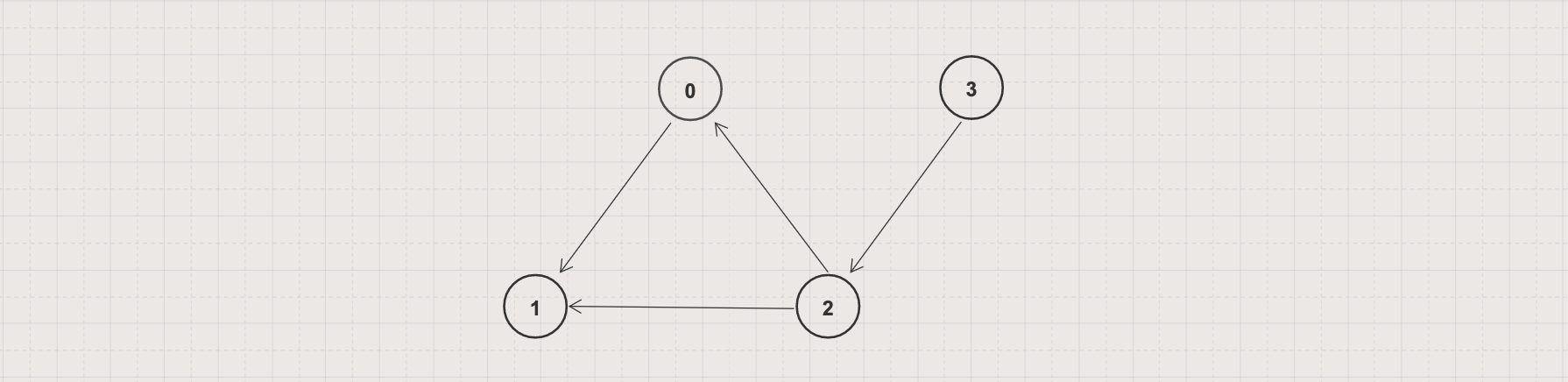
Output: [3, 2, 0, 1]
Explanation: [3, 2, 1, 0] is also a valid topological ordering
Example 2
- Input: Given a directed graph G = (V, E) with V = 5 and E = [[0, 1], [1, 2], [2, 0], [1, 3], [2, 4]]

Output: []
Explanation: No topological orderings exist as [0, 1], [1, 2], and [2, 0] formed a cycle. Vertex 0 can not both precede and follow vertex 2
Approach 1: DFS Iterative with Color
Run DFS Iterative with Color to find a vertex with no outgoing edges (Black vertex) and add it to a stack S. Stop finding when found a cycle
Repeat for all other vertices in the graph
Convert S to a list to get the final result
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class TopologicalSortByDFSIterativeColor {
static final int WHITE = 0, GRAY = 1, BLACK = 2;
static List<Integer> topologicalSort(GraphDirectedByAdjacencyList g) {
int[] color = new int[g.getV()];
Deque<Integer> stack = new ArrayDeque<>(g.getV());
Deque<Integer> sorted = new ArrayDeque<>(g.getV());
for (int i = 0; i < g.getV(); i++) {
if (color[i] != WHITE) continue;
stack.push(i);
while (!stack.isEmpty()) {
int v = stack.peek();
if (color[v] == WHITE) {
color[v] = GRAY;
} else {
color[v] = BLACK;
sorted.push(stack.pop());
}
for (int w : g.getAdjacencyList().get(v)) {
if (color[w] == GRAY) {
// Found a cycle
return new ArrayList<>();
} else if (color[w] == WHITE) {
stack.push(w);
}
}
}
}
return new ArrayList<>(sorted);
}
static void printResult(List<Integer> sorted) {
if (sorted.isEmpty()) {
System.out.println("There are no topological orderings as the input graph is cyclic");
} else {
sorted.forEach((x) -> System.out.printf("%d ", x));
System.out.println();
}
}
public static void main(String[] args) {
GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 0);
g1.addEdge(1, 3);
g1.addEdge(2, 4);
printResult(topologicalSort(g1));
GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
g2.addEdge(0, 1);
g2.addEdge(2, 0);
g2.addEdge(2, 1);
g2.addEdge(3, 2);
printResult(topologicalSort(g2));
}
}
GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial
- Output
There are no topological orderings as the input graph is cyclic
3 2 0 1
Time complexity: O(V+E)
Space complexity: O(V)
Approach 2: DFS Recursive with Color
Run DFS Recursive with Color to find a vertex with no outgoing edges (Black vertex) and add it to a stack S. Stop finding when found a cycle
Repeat for all other vertices in the graph
Convert S to a list to get the final result
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class TopologicalSortByDFSRecursiveColor {
static final int WHITE = 0, GRAY = 1, BLACK = 2;
static boolean hasCycle = false;
static void topologicalSortByDFSRecursive(GraphDirectedByAdjacencyList g, int v, int[] color, Deque<Integer> stack) {
if (hasCycle) {
return;
}
color[v] = GRAY;
for (Integer w : g.getAdjacencyList().get(v)) {
if (color[w] == GRAY) {
hasCycle = true;
}
if (color[w] == WHITE) {
topologicalSortByDFSRecursive(g, w, color, stack);
}
}
color[v] = BLACK;
stack.push(v);
}
static List<Integer> topologicalSort(GraphDirectedByAdjacencyList g) {
int[] color = new int[g.getV()];
Deque<Integer> stack = new ArrayDeque<>();
hasCycle = false;
for (int i = 0; i < g.getV(); i++) {
if (color[i] == WHITE) {
topologicalSortByDFSRecursive(g, i, color, stack);
}
}
return hasCycle ? new ArrayList<>() : new ArrayList<>(stack);
}
static void printResult(List<Integer> sorted) {
if (sorted.isEmpty()) {
System.out.println("There are no topological orderings as the input graph is cyclic");
} else {
sorted.forEach((x) -> System.out.printf("%d ", x));
System.out.println();
}
}
public static void main(String[] args) {
GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 0);
g1.addEdge(1, 3);
g1.addEdge(2, 4);
printResult(topologicalSort(g1));
GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
g2.addEdge(0, 1);
g2.addEdge(2, 0);
g2.addEdge(2, 1);
g2.addEdge(3, 2);
printResult(topologicalSort(g2));
}
}
GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial
- Output
There are no topological orderings as the input graph is cyclic
3 2 0 1
Time complexity: O(V+E)
Space complexity: O(V)
Approach 3: In-degree
Find a vertex with no incoming edges (in-degree = 0) and add it to a queue Q
Repeat for all other vertices in the graph
Convert Q to a list to get the final result
import java.util.*;
public class TopologicalSortByInDegree {
static List<Integer> topologicalSortByInDegree(GraphDirectedByAdjacencyList g) {
List<Integer> sorted = new ArrayList<>();
int[] inDegree = new int[g.getV()];
for (int v = 0; v < g.getV(); v++) {
for(int w : g.getAdjacencyList().get(v)) {
inDegree[w] += 1;
}
}
Queue<Integer> queue = new ArrayDeque<>();
for (int v = 0; v < g.getV(); v++) {
if (inDegree[v] == 0) {
queue.offer(v);
}
}
while (!queue.isEmpty()) {
int v = queue.poll();
sorted.add(v);
for (int w : g.getAdjacencyList().get(v)) {
inDegree[w]--;
if (inDegree[w] == 0) {
queue.offer(w);
}
}
}
return sorted.size() == g.getV() ? sorted : new ArrayList<>();
}
static void printResult(List<Integer> sorted) {
if (sorted.isEmpty()) {
System.out.println("There are no topological orderings as the input graph is cyclic");
} else {
sorted.forEach((x) -> System.out.printf("%d ", x));
System.out.println();
}
}
public static void main(String[] args) {
GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 0);
g1.addEdge(1, 3);
g1.addEdge(2, 4);
printResult(topologicalSortByInDegree(g1));
GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
g2.addEdge(0, 1);
g2.addEdge(2, 0);
g2.addEdge(2, 1);
g2.addEdge(3, 2);
printResult(topologicalSortByInDegree(g2));
}
}
GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial
- Output
There are no topological orderings as the input graph is cyclic
3 2 0 1
Time complexity: O(V+E)
Space complexity: O(V)
