Heap is a tree-based data structure in which all nodes in the tree are in a specific order. There are 2 types of heap, typically:
- Max Heap: all parent node's values are greater than or equal to children node's values, root node value is the largest.
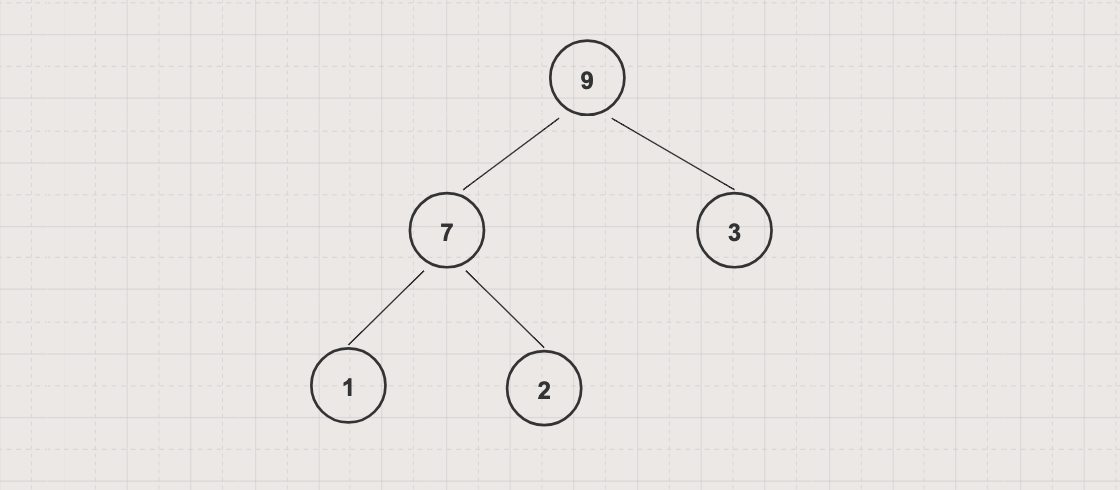
- Min Heap: all parent node's values are less than or equal to children node's values, root node value is the smallest.
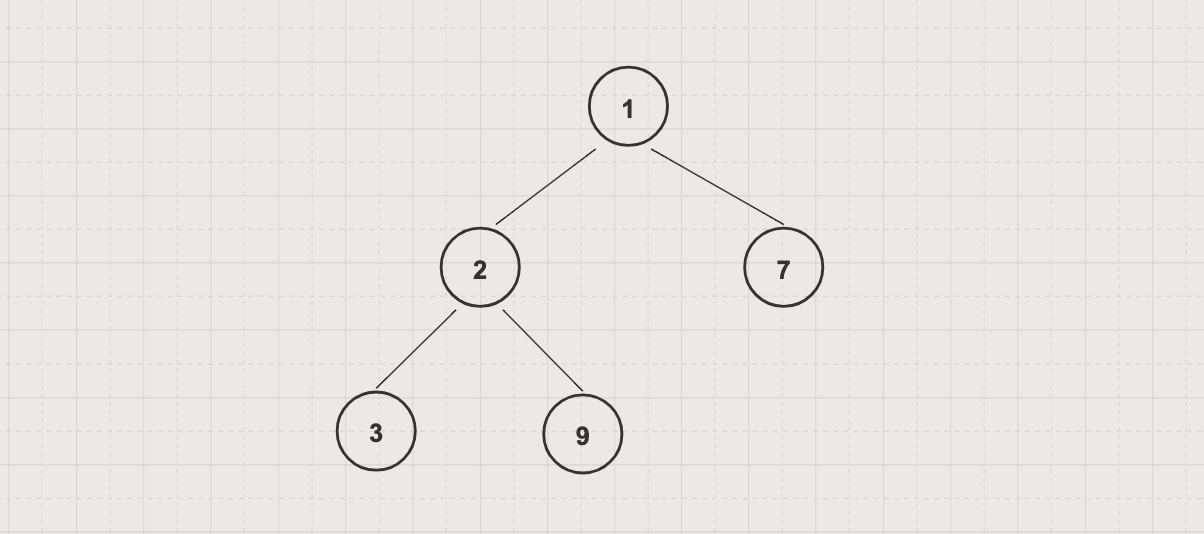
Basic operations
Insert aka Push: add a new node into the heap
Remove aka Pop: retrieves and removes the min or the max node of the heap
Examine aka Peek: retrieves without removes the min or the max node of the heap
Heapify: maintains max or min-heap property (all parent node's values should be greater/less than or equal to the child node's values)
Implementations
A common implementation of a heap is the binary heap which based on binary tree data structure
You can implement a binary heap with either a static array (capacity restricted) or a dynamic array
Binary Max Heap implementation example with Static Array
- Represented by 1-based integer array A[N+1]
- With a node A[k] (1<=k<=N)
- Its parent is A[k/2]
- Left child is A[k*2] (k*2 <= N)
- Right child is A[k*2+1] (k*2+1 <= N)
- A[1] is root node, A[0] is
Integer.MAX_VALUE
public class MaxHeapByArray {
private int[] heap;
private int size;
public MaxHeapByArray(int capacity) {
this.heap = new int[capacity+1];
this.heap[0] = Integer.MAX_VALUE;
this.size = 0;
}
private void swap(int i, int j) {
int tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
private void heapifyDown(int k) {
int largest = k;
int leftIndex = 2*k;
int rightIndex = 2*k + 1;
if (leftIndex <= heap.length && heap[leftIndex] > heap[largest]){
largest = leftIndex;
}
if (rightIndex <= heap.length && heap[rightIndex] > heap[largest]) {
largest = rightIndex;
}
if (largest != k) {
swap(k, largest);
heapifyDown(largest);
}
}
private void heapifyUp(int k) {
while (heap[k] > heap[k/2]) {
swap(k , k/2);
k = k/2;
}
}
private void print(){
for (int i = 1; i <= size/2; i++) {
System.out.printf("Parent: %d, Left child: %d, Right child: %d %s", heap[i], heap[i*2], heap[i*2+1], System.lineSeparator());
}
}
public void push(int x) {
heap[++size] = x;
heapifyUp(size);
}
public int pop() {
int head = heap[1];
heap[1] = heap[size--];
heapifyDown(1);
return head;
}
public int peek() {
return heap[1];
}
public static void main(String[] args) {
MaxHeapByArray maxHeap = new MaxHeapByArray(5);
maxHeap.push(3);
maxHeap.push(1);
maxHeap.push(7);
maxHeap.push(2);
maxHeap.push(9);
maxHeap.print();
System.out.println(maxHeap.peek());
System.out.println(maxHeap.pop());
System.out.println(maxHeap.peek());
}
}
Binary Min Heap implementation example with Static Array
Represented by 1-based integer array A[N+1]
With a node A[k] (1<=k<=N)
Its parent is A[k/2]
Left child is A[k*2] (k*2 <= N)
Right child is A[k*2+1] (k*2+1 <= N)
A[1] is root node, A[0] is
Integer.MIN_VALUE
public class MinHeapByArray {
private int[] heap;
private int size;
public MinHeapByArray(int capacity) {
this.heap = new int[capacity+1];
this.heap[0] = Integer.MIN_VALUE;
this.size = 0;
}
private void swap(int i, int j) {
int tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
private void heapifyDown(int k) {
int smallest = k;
int leftIndex = 2*k;
int rightIndex = 2*k + 1;
if (leftIndex <= heap.length && heap[leftIndex] < heap[smallest]){
smallest = leftIndex;
}
if (rightIndex <= heap.length && heap[rightIndex] < heap[smallest]) {
smallest = rightIndex;
}
if (smallest != k) {
swap(k, smallest);
heapifyDown(smallest);
}
}
private void heapifyUp(int k) {
while (heap[k] < heap[k/2]) {
swap(k , k/2);
k = k/2;
}
}
private void print(){
for (int i = 1; i <= size/2; i++) {
System.out.printf("Parent: %d, Left child: %d, Right child: %d %s", heap[i], heap[i*2], heap[i*2+1], System.lineSeparator());
}
}
public void push(int x) {
heap[++size] = x;
heapifyUp(size);
}
public int pop() {
int head = heap[1];
heap[1] = heap[size--];
heapifyDown(1);
return head;
}
public int peek() {
return heap[1];
}
public boolean isEmpty() {
return size == 0;
}
public static void main(String[] args) {
MinHeapByArray minHeap = new MinHeapByArray(5);
minHeap.push(3);
minHeap.push(1);
minHeap.push(7);
minHeap.push(2);
minHeap.push(9);
minHeap.print();
System.out.println(minHeap.peek());
System.out.println(minHeap.pop());
System.out.println(minHeap.peek());
}
}
Applications
Heaps can be used to implement Priority Queues
Find the shortest paths between vertices in a Graph Data Structure
The shortest path is a path between two vertices in a graph such that the total sum of the weights of the constituent edges is minimum
You can implement an algorithm to find the shortest path by using a Min-Heap and Dijkstra algorithm
Heaps in Java
In Java, the binary heap data structure is used to implement priority queues including java.util.PriorityQueue and java.util.concurrent.PriorityBlockingQueue
