In this article, you will learn to implement Depth First Search (DFS) algorithm on a graph by using Java with iterative and recursive approaches
Depth First Search (DFS) is an algorithm for traversing or searching for a graph. The algorithm starts at an arbitrary node and explores as far as possible along each branch before backtracking
Let's get started!
Problem
Give an undirected/directed graph G(V, E)
Write a Depth-First search algorithm to print out each vertex value exactly once
Example
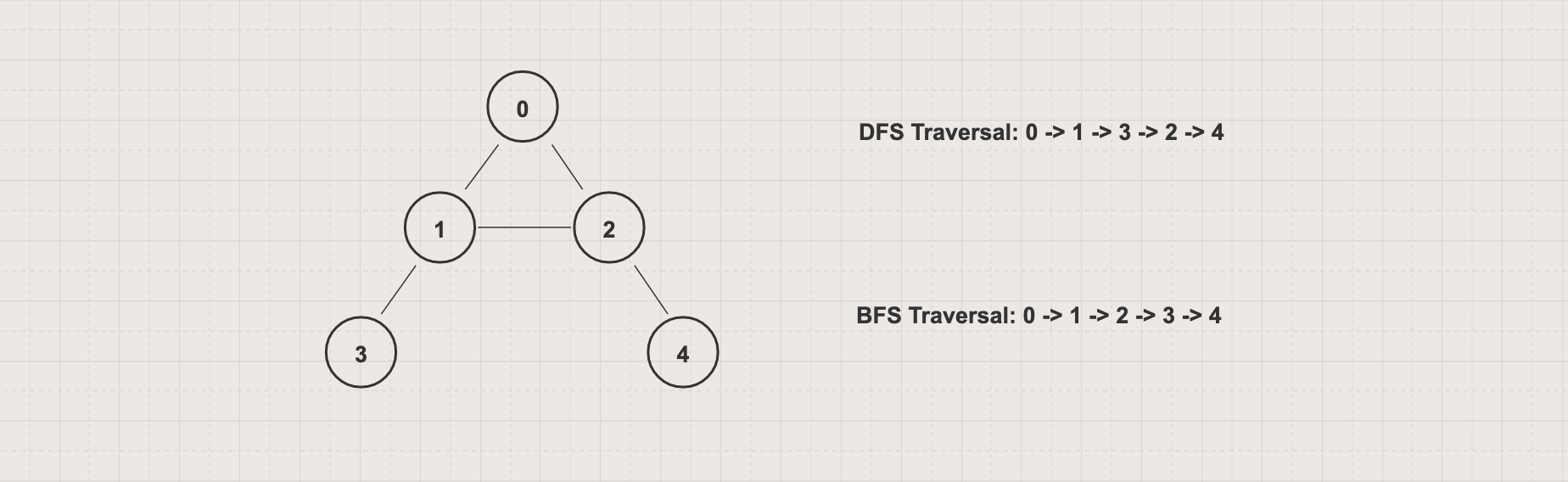
For the above graph with 0 as the starting vertex, assuming that the left edges are chosen before the right edges, the DFS traversal order will be 0 -> 1 -> 3 -> 2 -> 4
Approach 1: Iterative
Use an array to track visited nodes to avoid processing a node more than once
Use a stack to track which nodes to visit next
import java.util.ArrayDeque;
import java.util.Deque;
public class DFSByIterative {
static void dfsByIterative(GraphUndirectedByAdjacencyList g, int v) {
boolean[] visited = new boolean[g.getV()];
Deque<Integer> stack = new ArrayDeque<>();
stack.push(v);
while (!stack.isEmpty()) {
v = stack.pop();
if (!visited[v]) {
visited[v] = true;
System.out.printf("%d ", v);
for(Integer w : g.getAdjacencyList().get(v)) {
stack.push(w);
}
}
}
}
public static void main(String[] args) {
GraphUndirectedByAdjacencyList g = new GraphUndirectedByAdjacencyList(5);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(1, 0);
g.addEdge(1, 3);
g.addEdge(2, 4);
dfsByIterative(g, 0);
}
}
GraphUndirectedByAdjacencyList is defined in Graph Data Structure
- Output
0 1 3 2 4
Time complexity: O(V+E)
Space complexity: O(V)
Approach 2: Iterative with Color
Use a color array to track vertex states. Each vertex can have 3 states marked by color
White represents unvisited
Gray represents a visit in progress
Black represents visited
Use a stack to track which nodes to visit next
import java.util.ArrayDeque;
import java.util.Deque;
public class DFSByIterativeWithColor {
static final int WHITE = 0, GRAY = 1, BLACK = 2;
static void dfsByIterativeWithColor(GraphUndirectedByAdjacencyList g, int v) {
int[] color = new int[g.getV()];
Deque<Integer> stack = new ArrayDeque<>();
stack.push(v);
while (!stack.isEmpty()) {
v = stack.pop();
if (color[v] == WHITE) {
color[v] = GRAY;
System.out.printf("%d ", v);
for(Integer w : g.getAdjacencyList().get(v)) {
stack.push(w);
}
color[v] = BLACK;
}
}
}
public static void main(String[] args) {
GraphUndirectedByAdjacencyList g = new GraphUndirectedByAdjacencyList(5);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(1, 0);
g.addEdge(1, 3);
g.addEdge(2, 4);
dfsByIterativeWithColor(g, 0);
}
}
GraphUndirectedByAdjacencyList is defined in Graph Data Structure
- Output
0 1 3 2 4
Time complexity: O(V+E)
Space complexity: O(V)
Approach 3: Recursive
Use an array to track visited nodes to avoid processing a node more than once
Instead of using a stack, the DFS algorithm calls to itself to explore unvisited vertices
public class DFSByRecursive {
static void dfs(GraphUndirectedByAdjacencyList g, int v, boolean[] visited) {
visited[v] = true;
System.out.printf("%d ", v);
for (Integer w : g.getAdjacencyList().get(v)) {
if (!visited[w]) {
dfs(g, w, visited);
}
}
}
static void traversal(GraphUndirectedByAdjacencyList g) {
boolean[] visited = new boolean[g.getV()];
for (int i = 0; i < g.getV(); i++) {
if (!visited[i]) {
dfs(g, i, visited);
}
}
}
public static void main(String[] args) {
GraphUndirectedByAdjacencyList g = new GraphUndirectedByAdjacencyList(5);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(1, 0);
g.addEdge(1, 3);
g.addEdge(2, 4);
traversal(g);
}
}
GraphUndirectedByAdjacencyList is defined in Graph Data Structure
- Output
0 2 1 3 4
Time complexity: O(V+E)
Space complexity: O(V)
Approach 4: Recursive with Color
Use a color array to track vertex states. Each vertex can have 3 states marked by color
White represents unvisited
Gray represents a visit in progress
Black represents visited
Instead of using a stack, the DFS algorithm calls to itself to explore White vertices
public class DFSByRecursiveWithColor {
static final int WHITE = 0, GRAY = 1, BLACK = 2;
static void dfsByRecursiveWithColor(GraphUndirectedByAdjacencyList g, int v, int[] color) {
color[v] = GRAY;
System.out.printf("%d ", v);
for (Integer w : g.getAdjacencyList().get(v)) {
if (color[w] == WHITE) {
dfsByRecursiveWithColor(g, w, color);
}
}
color[v] = BLACK;
}
static void traversal(GraphUndirectedByAdjacencyList g) {
int[] color = new int[g.getV()];
for (int i = 0; i < g.getV(); i++) {
if (color[i] == WHITE) {
dfsByRecursiveWithColor(g, i, color);
}
}
}
public static void main(String[] args) {
GraphUndirectedByAdjacencyList g = new GraphUndirectedByAdjacencyList(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(2, 4);
traversal(g);
}
}
GraphUndirectedByAdjacencyList is defined in Graph Data Structure
- Output
0 2 1 3 4
Time complexity: O(V+E)
Space complexity: O(V)
Applications
Detect Cycle in a Directed Graph
You can use DFS to detect a cycle in a directed graph. When visiting a vertex v and its adjacency vertices, if there is a back edge (w, v) which directs to v then that graph has a cycle
Implement Topological Sort with Directed Acyclic Graph
Topological sort is an algorithm which takes a directed acyclic graph and returns a list of vertices in the linear ordering where each vertex has to precede all vertices it directs to
