Detect Cycle in a Directed Graph

In this article, we will learn to use Depth-First Search algorithms to detect a cycle in a directed graph

Unlike in an undirected graph, to detect a cycle in a directed graph, we should consider the edges direction

Problem

• Given a directed graph G = (V, E)

• Write an algorithm to detect a cycle in that graph

Example 1

• Input: Given a directed graph G = (V, E) with V = 5 and E = [[0, 1], [1, 2], [2, 0], [1, 3], [2, 4]]

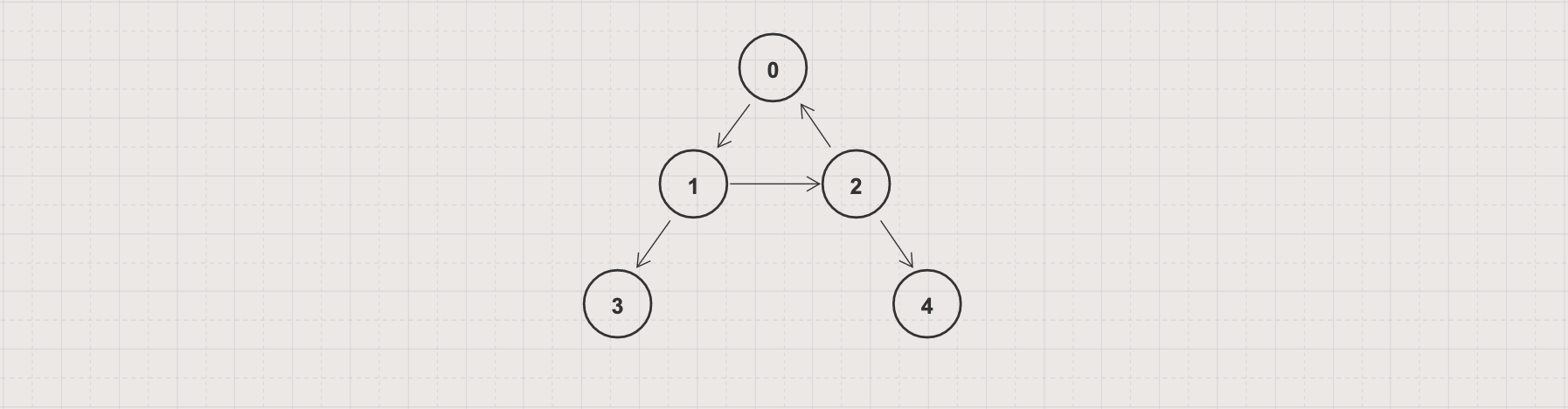
• Output: true

• Explanation: 3 edges [0, 1], [1, 2], [2, 0] formed a cycle

Example 2

• Input: Given a directed graph G = (V, E) with V = 4 and E = [[0, 1], [2, 0], [2, 1], [3, 2]]

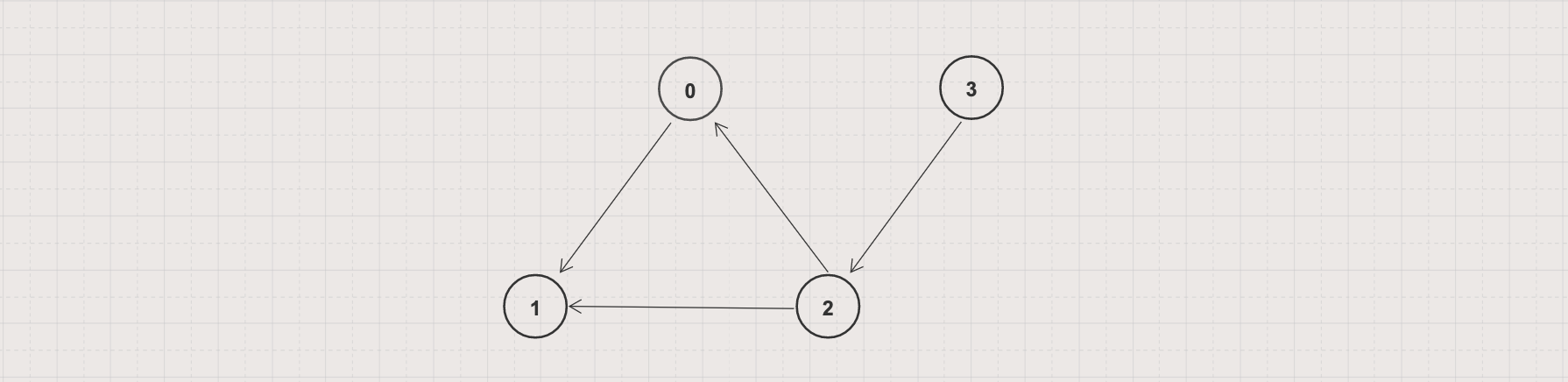
• Output: false

• Explanation: there are no cycles in the given graph

Approach 1: DFS Iterative

• Use a stack to track the traversal path

• Keeping track of the visited and on-stack state of each vertex

  While visiting a vertex and its adjacencies, if we ever encounter an on-stack vertex then the graph has a cycle

import java.util.ArrayDeque;  
import java.util.Deque;

public class DetectCycleDirectedByDFSIterative {  
    static boolean dfsByIterative(GraphDirectedByAdjacencyList g) {
        boolean[] visited = new boolean[g.getV()];
        boolean[] onStack = new boolean[g.getV()];
        Deque<Integer> stack = new ArrayDeque<>();

        for (int i = 0; i < g.getV(); i++) {
            if (visited[i]) continue;
            stack.push(i);

            while (!stack.isEmpty()) {
                int v = stack.peek();

                if (!visited[v]) {
                    visited[v] = true;
                    onStack[v] = true;
                } else {
                    onStack[v] = false;
                    stack.pop();
                }

                for (Integer w : g.getAdjacencyList().get(v)) {
                    if (!visited[w]) {
                        stack.push(w);
                    } else if (onStack[w]) {
                        return true;
                    }
                }
            }
        }

        return false;
    }

    public static void main(String[] args) {
        GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
        g1.addEdge(0, 1);
        g1.addEdge(1, 2);
        g1.addEdge(2, 0);
        g1.addEdge(1, 3);
        g1.addEdge(2, 4);
        System.out.println(dfsByIterative(g1));

        GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
        g2.addEdge(0, 1);
        g2.addEdge(2, 0);
        g2.addEdge(2, 1);
        g2.addEdge(3, 2);
        System.out.println(dfsByIterative(g2));
    }
}

GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial

• Output

true  
false

• Time complexity: O(V+E)

• Space complexity: O(V)

Approach 2: DFS Recursive

• Instead of using a stack, the algorithm calls to itself to explore unvisited vertices

• Keeping track of the visited and on-stack state of each vertex

  While visiting a vertex and its adjacencies, if we ever encounter an on-stack vertex then the graph has a cycle

import java.util.List;

public class DetectCycleDirectedByDFSRecursive {  
    static boolean dfsByRecursive(GraphDirectedByAdjacencyList g, int v, boolean[] visited, boolean[] onStack) {
        if (onStack[v]) return true;
        if (visited[v]) return false;

        visited[v] = true;
        onStack[v] = true;

        List<Integer> children = g.getAdjacencyList().get(v);
        for (Integer c: children) {
            if (dfsByRecursive(g, c, visited, onStack)) {
                return true;
            }
        }

        onStack[v] = false;
        return false;
    }

    static boolean hasCycle(GraphDirectedByAdjacencyList g) {
        boolean[] visited = new boolean[g.getV()];
        boolean[] onStack = new boolean[g.getV()];

        for (int i = 0; i < g.getV(); i++) {
            if (dfsByRecursive(g, i, visited, onStack)) {
                return true;
            }
        }

        return false;
    }

    public static void main(String[] args) {
        GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
        g1.addEdge(0, 1);
        g1.addEdge(1, 2);
        g1.addEdge(2, 0);
        g1.addEdge(1, 3);
        g1.addEdge(2, 4);
        System.out.println(hasCycle(g1));

        GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
        g2.addEdge(0, 1);
        g2.addEdge(2, 0);
        g2.addEdge(2, 1);
        g2.addEdge(3, 2);
        System.out.println(hasCycle(g2));
    }
}

GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial

• Output

true  
false

• Time complexity: O(V+E)

• Space complexity: O(V)

Approach 3: DFS Iterative with Color

• Use a stack to track the traversal path

• Keeping track of the unvisited (White color), visit in progress (Gray color, the vertex is on the stack) and visited state (Black color) of each vertex.

  While visiting a vertex and its adjacencies, if we ever encounter a gray vertex then the graph has a cycle

import java.util.ArrayDeque;  
import java.util.Deque;

public class DetectCycleDirectedByDFSIterativeColor {  
    static final int WHITE = 0, GRAY = 1, BLACK = 2;

    static boolean dfsByIterativeWithColor(GraphDirectedByAdjacencyList g) {
        int[] color = new int[g.getV()];
        Deque<Integer> stack = new ArrayDeque<>(g.getV());

        for (int i = 0; i < g.getV(); i++) {
            if (color[i] != WHITE) continue;
            stack.push(i);

            while (!stack.isEmpty()) {
                int v = stack.peek();

                if (color[v] == WHITE) {
                    color[v] = GRAY;
                } else {
                    color[v] = BLACK;
                    stack.pop();
                }

                for (int w : g.getAdjacencyList().get(v)) {
                    if (color[w] == GRAY) {
                        return true;
                    } else if (color[w] == WHITE) {
                        stack.push(w);
                    }
                }
            }
        }

        return false;
    }

    public static void main(String[] args) {
        GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
        g1.addEdge(0, 1);
        g1.addEdge(1, 2);
        g1.addEdge(2, 0);
        g1.addEdge(1, 3);
        g1.addEdge(2, 4);
        System.out.println(dfsByIterativeWithColor(g1));

        GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
        g2.addEdge(0, 1);
        g2.addEdge(2, 0);
        g2.addEdge(2, 1);
        g2.addEdge(3, 2);
        System.out.println(dfsByIterativeWithColor(g2));
    }
}

GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial

• Output

true  
false

• Time complexity: O(V+E)

• Space complexity: O(V)

Approach 4: DFS Recursive with Color

• Instead of using a stack, the algorithm calls to itself to explore unvisited vertices

• Keeping track of the unvisited (White color), visit in progress (Gray color, the vertex is on the stack) and visited state (Black color) of each vertex

  While visiting a vertex and its adjacencies, if we ever encounter a gray vertex then the graph has a cycle

public class DetectCycleDirectedByDFSRecursiveColor {  
    static final int WHITE = 0, GRAY = 1, BLACK = 2;

    static boolean dfsByRecursiveWithColor(GraphDirectedByAdjacencyList g, int v, int[] color) {
        color[v] = GRAY;

        for (Integer w : g.getAdjacencyList().get(v)) {
            if (color[w] == GRAY) {
                return true;
            }

            if (color[w] == WHITE && dfsByRecursiveWithColor(g, w, color)) {
                return true;
            }
        }

        color[v] = BLACK;
        return false;
    }

    static boolean hasCycle(GraphDirectedByAdjacencyList g) {
        int[] color = new int[g.getV()];

        for (int i = 0; i < g.getV(); i++) {
            if (color[i] == WHITE && dfsByRecursiveWithColor(g, i, color)) {
                return true;
            }
        }

        return false;
    }

    public static void main(String[] args) {
        GraphDirectedByAdjacencyList g1 = new GraphDirectedByAdjacencyList(5);
        g1.addEdge(0, 1);
        g1.addEdge(1, 2);
        g1.addEdge(2, 0);
        g1.addEdge(1, 3);
        g1.addEdge(2, 4);
        System.out.println(hasCycle(g1));

        GraphDirectedByAdjacencyList g2 = new GraphDirectedByAdjacencyList(4);
        g2.addEdge(0, 1);
        g2.addEdge(2, 0);
        g2.addEdge(2, 1);
        g2.addEdge(3, 2);
        System.out.println(hasCycle(g2));
    }
}

GraphDirectedByAdjacencyList is defined in Graph Data Structure Tutorial

• Output

true  
false

• Time complexity: O(V+E)

• Space complexity: O(V)